かつて世界のナベアツは、3の倍数と3の付く数字のときだけアホになったといいます。世界のナベアツがひたすらに数を数え続けるとアホになる割合が1に近づいていくというのは有名な話(?)ですが、もしナベアツの生態が「ゾロ目のときだけアホになる」というものだったなら、ナベアツはどのくらいアホになっていたのでしょうか?
本物の世界のナベアツが\(k\)桁まで数えたときにアホになる割合は、次の式で与えられます(参考:ナベアツ方程式):$$ 1 - \frac{2 \cdot 3^{2k-1} - 1}{10^k} $$この式の値は\(k\)を無限大に飛ばすと\(1\)に収束するので、「アホになる割合が1に近づいていく」のだと言える訳です(実際にはもっと簡単に言えます)。ではゾロ目のナベアツはどうでしょう。
ゾロ目のときだけアホになるゾロ目ナベアツが、\(k\)桁の数を数えているときを考えます。\(k\)桁の数は\(9 \cdot 10^{k-1}\)個あります(先頭の桁は\(0\)でありえないため)が、そのうちゾロ目の数は\(9\)個です。実際には\(1\)桁から\(k\)桁まで数え上げる訳ですから、総和を取って\(\sum^{k}_{i=1} 9 \cdot 10^{k-1}\)個の数のうち\(9k\)個がゾロ目であるということになります。前者は$$ \begin{align*} \sum^{k}_{i=1} 9 \cdot 10^{k-1} &= 9 \cdot \frac{10^0 (10^k - 1)}{10 - 1} \\ &= 10^k - 1 \\ \end{align*} $$となって、ゾロ目ナベアツがアホになる割合は$$ \frac{9k}{10^k - 1} $$だということになりました。順当に少ないですね。\(k\)を無限大に飛ばすと\(0\)に収束します。各桁での「アホ率」も\(\frac{1}{10^{k-1}}\)で与えられるので、どんどん正気を取り戻していくみたいですね。良かったです。
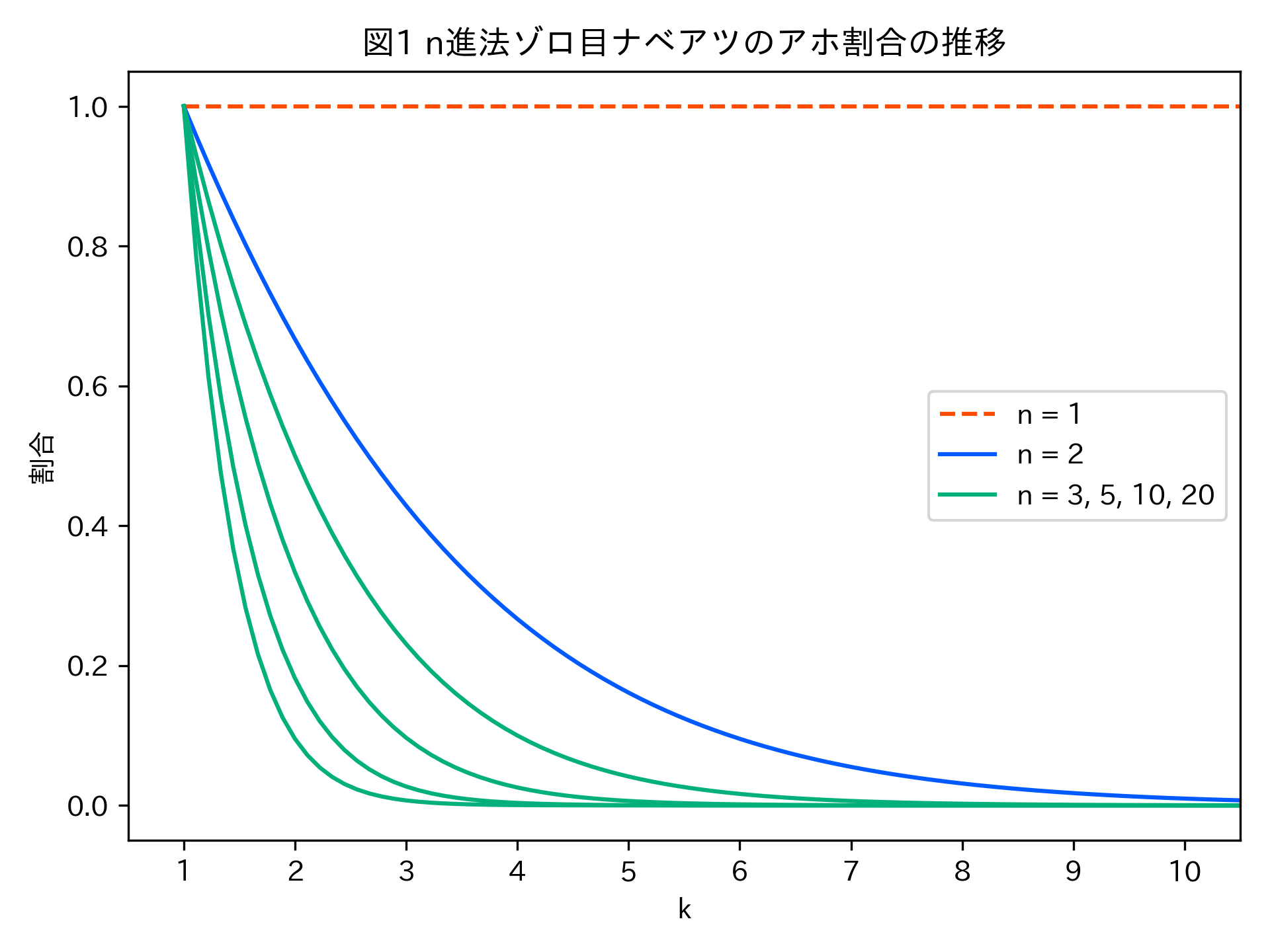
……ところで、このゾロ目ナベアツは10進法の世界に生きています。しかし、並行世界のゾロ目ナベアツは必ずしもそうではありません。正確に言うと、並行世界は可算無限個あり、またゾロ目ナベアツは各世界に一人ずつしかいません。さらに全てのゾロ目ナベアツは相異なる位取りを用いているので、\(n\)進法を使うゾロ目ナベアツを\(X_n\)として数え上げることができます。今まで見てきた10進法ゾロ目ナベアツは\(X_{10}\)さんだったんですね。ほとんどの並行ゾロ目ナベアツは、\(k\)桁まで数えたときに各桁$$ \frac{1}{n^{k-1}} $$の割合でアホになり、累積$$ \frac{k(n-1)}{n^k - 1} $$の割合でアホになることが、先程と同様の計算でわかります。やはり正気になっていってくれるようで嬉しいです。

ここで「ほとんどの並行ゾロ目ナベアツ」といったのは、具体的には\(n > 1\)の範囲の\(X_n\)です。つまり、\(X_1\)だけはこの限りでないということです。1進法が何者かということは考える必要がありますが、ここでは1をN個並べることでNを表す記数法のことだとしておきます。定義されないとすると\(X_1\)さんが消滅してしまって悲しいので…… \(X_1\)は、1つの数字しか使えない以上、発する数は常にゾロ目になることになります。つまり、常にアホであり続けるということです。それもまた一興ですね。
1進法の定義はともかく、\(X_n (n>1)\)からの推測として、\(X_1\)が割合\(1\)でアホになる存在なのは妥当なことに思えます。\(X_n\)がアホになる割合は\(n\)が大きくなればなるほど速く0に近づいていき、逆に\(n\)が小さくなるほど収束は遅くなります。その極限が「限りなく収束の遅い」=いつまでもアホであり続ける\(X_1\)なのではないでしょうか?
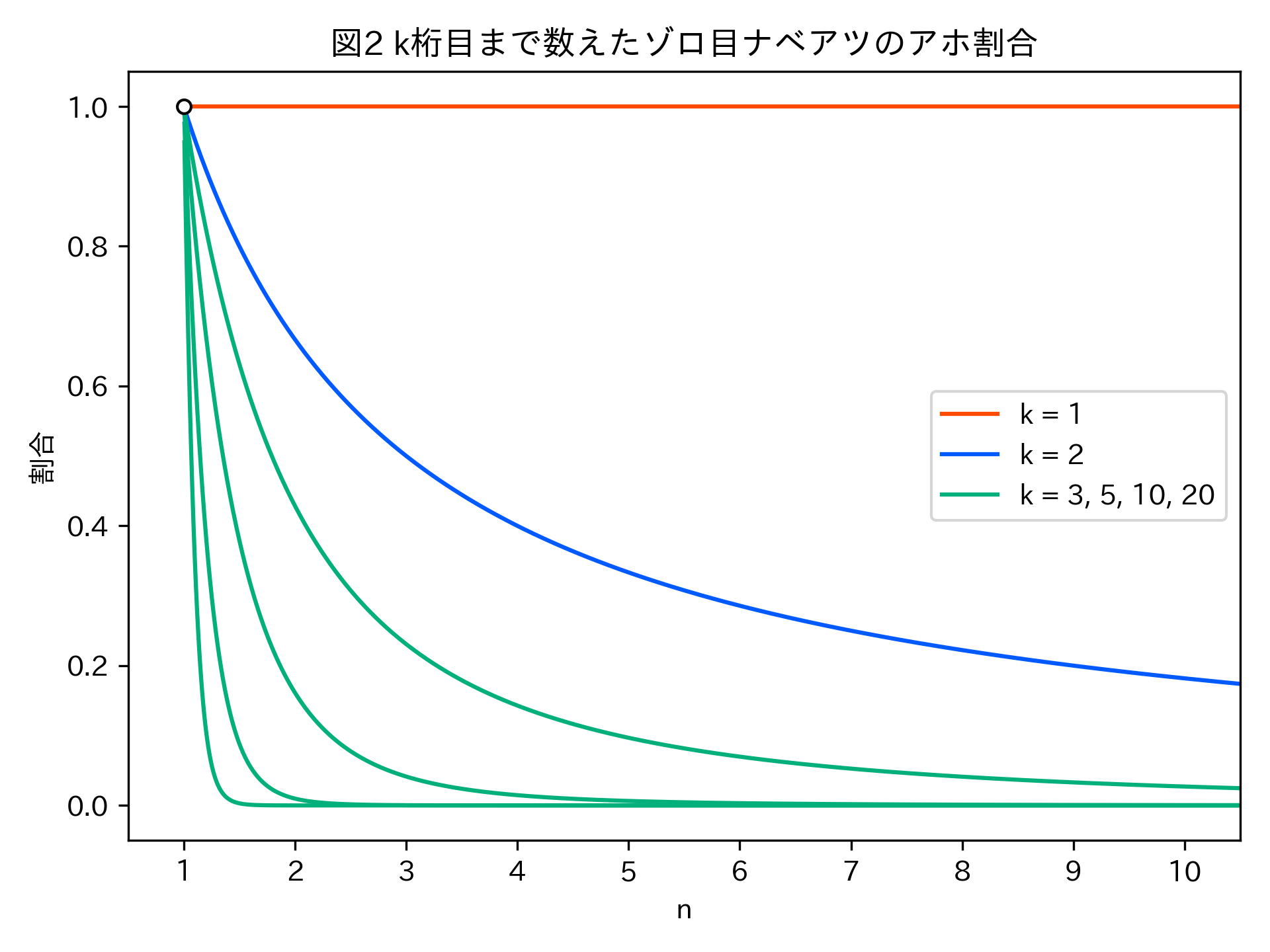
確かめてみましょう。\(\frac{k(n-1)}{n^k - 1}\)は\(n=1\)で不定形となり、定義されません。そこで\( \lim_{n \to 1} \frac{k(n-1)}{n^k - 1} \)を考える訳ですが、数学から離れて久しい私には計算方法がさっぱり思いつきませんでした。そこでGeminiに訊いてみると、次のような証明を与えてくれました:
- \(f(x) = x^k\)とする。
- このとき$$ \begin{align*} f'(1) &= \lim_{n \to 1} \frac{f(n) - f(1)}{n-1} \\ &= \lim_{n \to 1} \frac{n^k - 1}{n-1} \end{align*} $$である。
- ところで\(f'(x) = kx^{k-1}\)から$$ f'(1) = k $$である。
- 従って$$ \begin{align*} k &= \lim_{n \to 1} \frac{n^k - 1}{n-1} \\ \frac{1}{k} &= \lim_{n \to 1} \frac{n-1}{n^k - 1} \\ 1 &= \lim_{n \to 1} \frac{k(n-1)}{n^k - 1} \\ \end{align*} $$となり解が得られる。
かしこ〜。美しいですね。思いつける気がしません。ところでGeminiに訊く前に、友人にもメッセージを投げていました。友人が返してくれた証明は次のようなものでした:$$ \begin{align*} \lim_{n \to 1} \frac{k(n-1)}{n^k - 1} &= \lim_{n \to 1} \frac{k(n-1)}{(n-1)(n^{k-1} + n^{k-2} + \cdots + n^0)} \\ &= \lim_{n \to 1} \frac{k}{n^{k-1} + n^{k-2} + \cdots + n^0} \\ &= \frac{k}{k} \\ &= 1 \\ \end{align*} $$かしこ〜。美しいですね。こっちは高三の頃の私だったら思いつけていた気もします。
いずれにせよ、$$ \lim_{n \to 1} \frac{k(n-1)}{n^k - 1} = 1 $$であることがわかりました。従って、1進法ゾロ目ナベアツ\(X_1\)は\(k\)の値に関わらず割合\(1\)でアホになると考えるべきでしょう。やはり\(X_1\)さんだけは、アホになり続ける運命から逃れられないようですね……